Deoarece între matematică şi muzică este o strânsă legătură, iar muzica este ingredientul nelipsit atunci când vine vorba de dans, este firesc să ne gândim că matematica şi arta dansului nu sunt tocmai străine una de alta.

Ce face un începător atunci când învaţă să danseze vals? Numără paşii: 1, 2, 3, 1, 2, 3, 1, 2, 3, ... în ritmul muzicii. Deci mişcările specifice valsului formează un şir ale cărui elemente se repetă din 3 în 3. De obicei, mişcările mai accentuate sunt cele care cad pe timpii accentuaţi ai muzicii. În cazul valsului, mişcările accentuate sunt cele corespunzătoare cifrei 1. Iar în cazul dansatorilor profesionişti, traiectoriile descrise de aceştia pe podea în timpul dansului formează figuri geometrice complexe.

Matematica se găseşte în ritm, în împărţirea dansatorilor pe grupe, în folosirea spaţiului sau în forma şi succesiunea mişcărilor pe care le face un dansator. Putem astfel spune că matematica este implicată în toate aspectele dansului. De aceea, mai multe instituţii educaţionale din întreaga lume au început să folosească acest lucru într-o manieră interdisciplinară.

Pornind de la legătura dansului cu matematica, profesorii americani Karl Schaffer şi Erik Stern au înfiinţat organizaţia Math Dance, care are ca scop promovarea matematicii şi dansului ca fiind o activitate creativă unitară, şi nu două discipline separate. Ei consideră că ideile matematice sunt mai atractive, mai uşor de înţeles şi de reţinut atunci când sunt exprimate prin intermediul propriului nostru corp.

De exemplu, să vedem cum putem obţine un dans pornind de la numele cuiva. Orice cuvânt este format din vocale şi consoane. Pentru fiecare vocală vom bate o dată din palme, pentru fiecare consoană vom lovi o dată cu palmele pe coapse, iar prima literă a numelui o vom accentua printr-o lovitură mai sonoră. Dacă repetăm numele de mai multe ori la rând, obţinem o succesiune de mişcări şi un ritm specific acelui nume. Pentru a crea un ritm mai complex, putem alătura doi participanţi care-şi „dansează” numele simultan, începând în acelaşi moment şi având acelaşi tempo. Urmărindu-i, ne putem întreba după câte mişcări vor face amândoi o mişcare accentuată în acelaşi timp (exceptând mişcarea accentuată de la început)? Se introduce astfel noţiunea de „cel mai mic multiplu comun” (ritmul a două nume cu lungimea de 4, respectiv 6 litere, va avea mişcări accentuate simultan după 12 mişcări, 12 fiind cel mai mic multiplu comun al numerelor 4 şi 6).

 Bătăile palmelor din exemplul de mai sus pot fi înlocuite cu mişcări de dans din ce în ce mai complexe, până la obţinerea unui dans în toată regula. O altă metodă de a obţine un dans matematic este aceea care presupune folosirea unei panglici lungi şi implică mai mulţi participanţi. Scopul este ca dansatorii să construiască forme geometrice cu ajutorul panglicii care uneşte corpurile lor, făcând prin dans tranziţia între diversele forme geometrice. De exemplu, participanţii încep cu un pătrat, continuă cu un triunghi dreptunghic, apoi cu un trapez isoscel şi încheie prin apariţia unui hexagon.

Dansul este o formă de expresie prin mişcarea corpului. Iar corpul uman este simetric, poate de aceea preferăm, din punct de vedere estetic, mişcările simetrice. În dans se întâlnesc toate tipurile de simetrie, majoritatea fiind puse cel mai bine în evidenţă printr-un grup de dansatori şi un conducător. Puteţi încerca următorul exerciţiu: alegeţi un lider şi cel puţin 3 participanţi, unde liderul poate fi poziţionat cu faţa sau cu spatele spre restul grupului. Liderul trebuie să numească un tip de simetrie, apoi să execute o mişcare simplă (cum ar fi să ridice o mână). Cei din restul grupului trebuie să execute mişcarea liderului, dar în mod simetric faţă de acesta. Dansul se poate continua cu mişcări din ce în ce mai complexe, apoi alternând tipurile de simetrie.

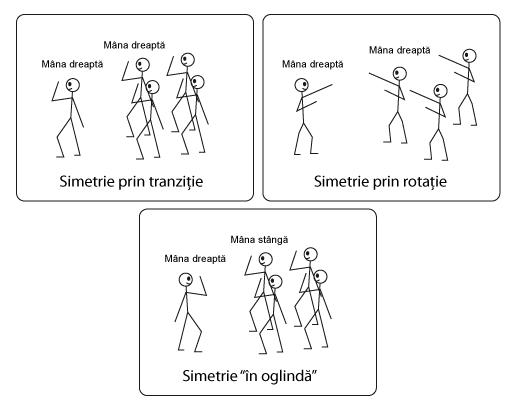
 Bineînţeles, toate cele enumerate mai sus sunt doar câteva modalităţi prin care se poate evidenţia legătura matematicii cu dansul. Pe celelalte le puteţi descoperi singuri dacă, data viitoare când vă confruntaţi cu un concept matematic, vă veţi întreba: „Oare cum aş putea dansa asta?”